标题：探索热门函数图像：从基本到高级

引言

函数图像是数学和科学领域中的重要工具，它能够帮助我们直观地理解函数的性质和行为。在数学教育、科学研究以及工程实践中，函数图像的应用无处不在。本文将带您探索一些热门的函数图像，从基本的三角函数到复杂的混沌函数，让我们一同揭开这些图像背后的数学奥秘。

基本函数图像

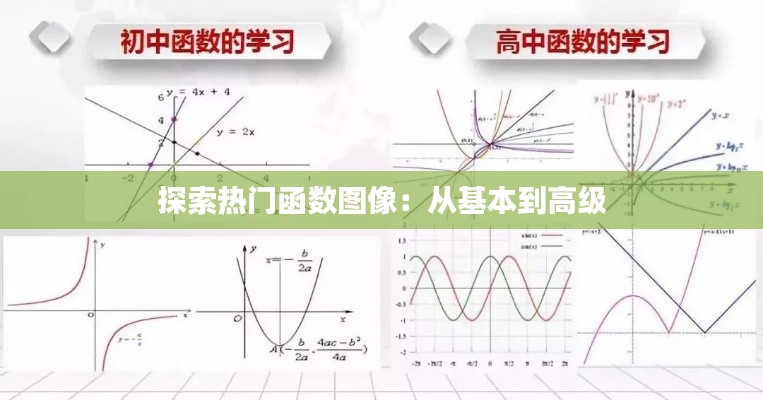
在数学中，最基本的函数图像包括线性函数、二次函数、指数函数和对数函数等。以下是一些常见的函数图像及其特点：

线性函数

线性函数的图像是一条直线，其一般形式为y = mx + b，其中m是斜率，b是y轴截距。线性函数图像的特点是斜率恒定，图像呈直线状。

二次函数

二次函数的图像是一个抛物线，其一般形式为y = ax^2 + bx + c，其中a、b、c是常数。当a > 0时，抛物线开口向上；当a

指数函数

指数函数的图像呈现指数增长或衰减的趋势，其一般形式为y = a^x，其中a是底数。指数函数图像的特点是随着x的增加，y值会呈指数级增长或衰减。

对数函数

对数函数的图像呈现对数增长或衰减的趋势，其一般形式为y = log_a(x)，其中a是底数。对数函数图像的特点是随着x的增加，y值会呈对数级增长或衰减。

三角函数图像

三角函数是数学中非常重要的函数，它们在物理学、工程学等领域有着广泛的应用。以下是一些常见的三角函数图像及其特点：

正弦函数

正弦函数的图像是一个周期性的波形，其一般形式为y = sin(x)。正弦函数图像的特点是周期为2π，振幅为1，图像在x轴两侧对称。

余弦函数

余弦函数的图像也是一个周期性的波形，其一般形式为y = cos(x)。余弦函数图像的特点是周期为2π，振幅为1，图像在x轴两侧对称，且比正弦函数图像滞后π/2。

正切函数

正切函数的图像是一个周期性的曲线，其一般形式为y = tan(x)。正切函数图像的特点是周期为π，振幅无限大，图像在y轴两侧有垂直渐近线。

高级函数图像

随着数学的发展，一些高级函数图像逐渐成为研究热点。以下是一些有趣的函数图像：

混沌函数

混沌函数是一种具有确定性但复杂行为的函数。著名的混沌函数有Logistic映射和Lorenz系统。混沌函数图像的特点是具有分形结构，看似随机但又有规律可循。

双曲函数

双曲函数是指数函数的对数函数，包括双曲正弦、双曲余弦和双曲正切等。双曲函数图像的特点是具有类似三角函数的周期性和对称性，但振幅和周期与三角函数不同。

结论

函数图像是数学中不可或缺的工具，它们帮助我们更好地理解函数的性质和行为。从基本的线性函数到复杂的混沌函数，每一个函数图像都蕴含着丰富的数学内涵。通过探索这些函数图像，我们可以更深入地了解数学世界的奇妙之处。